Pí jégkocka forma

Pí öv

Négyszázhetvenkét éve, 1540. január 28-án született Ludolph van Ceulen, akinek nevét az tette halhatatlanná, hogy 35 tizedesjegyig számította ki a pi értékét.

Azok kedvéért, akik már régen jártak iskolába: a pi a kör területének és rületének kiszámításához használt konstans érték, a kör kerületének és átmérőjének hányadosa, amely a kör nagyságától független állandó szám. Azt már az ókorban is tudták, hogy e szám nagyjából 3-nak felel meg, a matematikában is jeleskedő Arisztotelész a körbe írt és a köré írt sokszögek kerületének határértékeivel 3 10/70 és 3 10/71 között adta meg, ami nagyjából 3,141-nek felel meg. A bűvös szám meghatározásával ezután is sokan próbálkoztak, segítségül híva a kör (ma már tudjuk, reménytelen) négyszögesítését is.

E probléma izgatta Ceulent is, aki nevével ellentétben nem Kölnben, hanem Hildesheimben született. Szüleinek szegénysége miatt egyetemre nem járt, így a korabeli latin és görög nyelven írt tudományos műveket csak fordításokból ismerte meg. Számos protestáns némethez hasonlóan a katolikus inkvizíció elől Hollandiába települt. Először Delft városában tanított matematikát és vívást, majd Leidenben nyitott vívóiskolát, később az itteni műszaki főiskolán adott elő matematikát, földmérést és hadiépítészetet 1610. december 31-én bekövetkezett haláláig.

Forrás: www.impulzus.ro/A_pi_kiszamitoja_470_eve_szuletett/hirek/13487

Te hány tizedesjegyig ismered a Pi-t ?

Ezen a napon született Einstein, s ennek kapcsán ünneplik minden évben a NEMZETKÖZI PI NAP-ot.

A matematika egyik leghíresebb száma 3.1415926535…-el kezdődik és a végtelenségig tart.

Minden évben különböző rendezvényekkel, vetélkedőkkel, konferenciákkal „ünneplik” a számot, számos könyv jelent meg már a témával kapcsolatban.

Négyszázhetven éve, 1540. január 28-án született Ludolph van Ceulen, akinek nevét az tette halhatatlanná, hogy 35 tizedesjegyig számította ki a pi értékét.

Azok kedvéért, akik már régen jártak iskolába: a pi a kör területének és rületének kiszámításához használt konstans érték, a kör kerületének és átmérőjének hányadosa, amely a kör nagyságától független állandó szám. Azt már az ókorban is tudták, hogy e szám nagyjából 3-nak felel meg, a matematikában is jeleskedő Arisztotelész a körbe írt és a köré írt sokszögek kerületének határértékeivel 3 10/70 és 3 10/71 között adta meg, ami nagyjából 3,141-nek felel meg. A bűvös szám meghatározásával ezután is sokan próbálkoztak, segítségül híva a kör (ma már tudjuk, reménytelen) négyszögesítését is.

E probléma izgatta Ceulent is, aki nevével ellentétben nem Kölnben, hanem Hildesheimben született. Szüleinek szegénysége miatt egyetemre nem járt, így a korabeli latin és görög nyelven írt tudományos műveket csak fordításokból ismerte meg. Számos protestáns némethez hasonlóan a katolikus inkvizíció elől Hollandiába települt. Először Delft városában tanított matematikát és vívást, majd Leidenben nyitott vívóiskolát, később az itteni műszaki főiskolán adott elő matematikát, földmérést és hadiépítészetet 1610. december 31-én bekövetkezett haláláig.

Forrás: www.impulzus.ro/A_pi_kiszamitoja_470_eve_szuletett/hirek/13487

A MathWorld(mathworld.wolfram.com) szerint a leggyorsabb algoritmus a Pi meghatározására a Chudnovsky algoritmus:

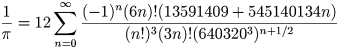
A mnemotechnikai verseknek egy fajtáját képezik az olyan versek (szövegek), amelyek számneveket nem is tartalmaznak, hanem a szöveg minden egyes szava betűinek száma szolgáltatja a megjegyzésre szánt számsorozatot. Ez utóbbi versek főleg sokjegyű szám, illetőleg hosszú tizedes tört számjegyeinek megjegyzésére alkalmasak, amennyiben a számjegyek között nincs nulla (hacsak nem akarjuk a "nullá"-t gondolatjellel kifejezni, ami a versköltő munkáját még jobban megnehezítené, vagy pedig 10 betűs szóval fejezni ki a zérót)

A jó pi-versek sok számjegyet adnak meg és szigorúan a tárgynál maradnak. Ezeknek a kritériumoknak csak igen kevés mű tud eleget tenni (az idegen nyelvű változatokat is beleértve).

Minden idők legjobb — a fenti kritériumoknak eleget tevő — magyar nyelvű pi-versét Szász Pál matematikus írta 1952-ben.

Forrás: members.iif.hu/visontay/ponticulus/rovatok/mnemonika/pi_vers.html

A PI sok olyan geometriai képletben szerepel, amelyek körökkel és gömbökkel kapcsolatosak.

Geometriai alakzat	Képlet
A kör kerülete r sugárból, d átmérőből
A kör területe r sugárból
Az ellipszis területe, a és b féltengelyekből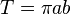
A gömb térfogata r sugárból, d átmérőből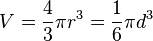
A gömb felülete r sugárból
A henger térfogata h magasságból és r alapsugárból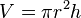
A henger felülete h magasságból és r alapsugárból
A kúp térfogata h magasságból és r alapsugárból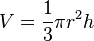
A kúp felülete h magasságból és r alapsugárból

Forrás: hu.wikipedia.org/wiki/Pi_%28sz%C3%A1m%29

Pi
(1998)

New York Manhattan városrészében, hét lakat alatt lakik Max Cohen, a paranoiás matematikus és komputerzseni. A hatéves kora óta kibírhatatlan fejfájással küszködő férfi képtelen kapcsolatot teremteni embertársaival, egyedül a számok és bitek birodalmában érzi otthon magát. Legújabb hobbija a tőzsdei kalkulációk világába vezeti - így figyel fel tehetségére a Wall Street. Hősünk így egyszerre kerül az elutasítást nem ismerő brókerek és a Tóra elveszett számmisztikai rejtélyeit kutató fiatalember, Lenny szorításába, miközben kínzó hallucinációi és migrénrohamai egyre erősebbé válnak. Vajon megoldást kínál-e a természet Max gondjaira és képes-e ő maga megtalálni ezeket?

Nemzet: amerikai
Stílus: sci-fi, thriller
Hossz: 85 perc
Magyar mozibemutató: 2003. szeptember 4.

Forrás: filmkatalogus.hu/Pi--f12461

Én a számítások során a QuickPi v4.5 programot használom.

A program letölthető a következő tárhelyek valamelyikéről:

Tükör 1:

members.shaw.ca/francislyster/pi/pi.html

Tükör 2:

 www.load.to/KGboRslgrT/qpi45.zip

Tükör 3:

addat.hu/95f72085/qpi45.zip.html

Program használata: parancssorból indítható, majd:

qpi digits[k|m|g] [destfile] [options|-h]

Példa: Pi számítás 1 millió tizedesjegy pontossággal, pi.txt állományba mentve:

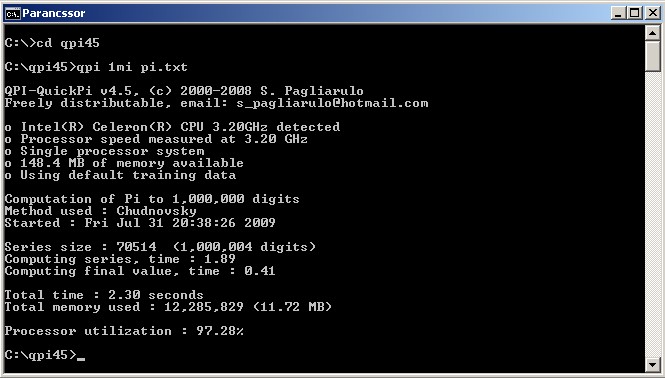
A Pi értéke 10 millió tizedesjegy pontossággal

Számítógéppel néhány perc alatt kiszámolható ilyen pontossággal...

Mivel ilyen hosszú bejegyzést nem lehet írni, ezért .txt formátumban lehet letölteni az alábbi tárhelyek valamelyikéről.

Méret: 13103 Kb

Tükör 1:

www.load.to/hV7uRBNblO/pi10mi.txt

Tükör 2:

 addat.hu/55ce3b53/pi10mi.txt.html

A Pi értéke 40000 tizedesjegy pontossággal

Pi = 3.
1415926535 8979323846 2643383279 5028841971 6939937510  : 50
5820974944 5923078164 0628620899 8628034825 3421170679  : 100
8214808651 3282306647 0938446095 5058223172 5359408128  : 150
4811174502 8410270193 8521105559 6446229489 5493038196  : 200
4428810975 6659334461 2847564823 3786783165 2712019091  : 250
4564856692 3460348610 4543266482 1339360726 0249141273  : 300
7245870066 0631558817 4881520920 9628292540 9171536436  : 350
7892590360 0113305305 4882046652 1384146951 9415116094  : 400
3305727036 5759591953 0921861173 8193261179 3105118548  : 450
0744623799 6274956735 1885752724 8912279381 8301194912  : 500

9833673362 4406566430 8602139494 6395224737 1907021798  : 550
6094370277 0539217176 2931767523 8467481846 7669405132  : 600
0005681271 4526356082 7785771342 7577896091 7363717872  : 650
1468440901 2249534301 4654958537 1050792279 6892589235  : 700
4201995611 2129021960 8640344181 5981362977 4771309960  : 750
5187072113 4999999837 2978049951 0597317328 1609631859  : 800
5024459455 3469083026 4252230825 3344685035 2619311881  : 850
7101000313 7838752886 5875332083 8142061717 7669147303  : 900
5982534904 2875546873 1159562863 8823537875 9375195778  : 950
1857780532 1712268066 1300192787 6611195909 2164201989  : 1000



Habár a Chudnovsky-testvérek semmire sem jutottak a π tizedesjegyeivel, úgy érzik, hogy a számítógépük segítségével megpillanthatnak valamit, ami előfutára lesz egy fontos felfedezésnek a π-ről vagy a transzcendentális számokról általában. Úgy, mint ahhoz, hogy sok mindent megtudjunk a macskákról, elég, ha egyetlen macskát közelről megvizsgálunk. Ha közelről kívánjuk megvizsgálni a π-t, hogy minél többet lássunk, hatalmas szuperszámítógépekre van szükség. Betáplálható-e az univerzum egy szuperszámítógépbe? És, ha igen? Milyen mélységben válik láthatóvá a π? Természetesen munkájuk során mindezeket a testvérek is figyelembe vették. Úgy képzelték, hog akkora gépet építenek, amelyben elfér az egész világegyetem. A méretét a következőképpen határozták meg. Az általunk észlelhető világegyetem körülbelül 10⁷⁹ elektront és protont tartalmaz, ez az úgynevezett Eddington-szám. (A világegyetem véges volta nem bizonyított. − a szerk.) (Sir Arthur Stanley Eddington, asztrofizikus volt, aki először meghatározta ezt a számot.) Az Eddington-számban az 1-est 79 nulla követi: